今回は物体検出モデルについて、最良のモデルの選択方法について検討していきます。
ここでのモデルの選択方法とは、どの物体検出モデル(YOLO, SSDなど)を選択するかということではありません。
データを学習させた後の予測段階において、どのエポック数のモデルを採用するかといった話になります。
一般的な機械学習では、train lossとval lossの推移からval lossが最も小さいエポック数のモデルを採用することが多いです。
それは、val lossが小さくなるほど学習がうまく進んでおり、精度も向上するだろうという前提があるからです。
しかし、場合によってはlossの値と精度に相関関係が見られない場合もあります。
また、モデルを選択する際、学習させたモデルの使用目的によっては、lossの値ではなく別の指標でモデルを選択する場合もあります。
そのため、一概にval lossの値が最も小さいモデルを採用すれば良いというわけではありません。
それでは、物体検出において、どのようにモデルを選択すべきか検討していきます。
モデルの選択基準① val lossとmAP(test data)
まず初めに、各epoch数におけるval lossの値と、テストデータに対するmAPの値の推移を比較してみます。
mAPとは物体検出モデルの精度を評価するための指標となっており、mAPの値(%)が高いほど精度が高いことを示しています。
詳しくは以下の記事を参照してください。

今回の場合、val lossの値が小さくなるにつれてmAPの値が大きくなっていれば、val lossとmAPの間に相関関係があると言えます。
それでは各々の物体検出モデル(Faster-R-CNN, SSD, YOLOv8)別にval lossとmAPの相関関係を確認していきます。
Faster-R-CNN
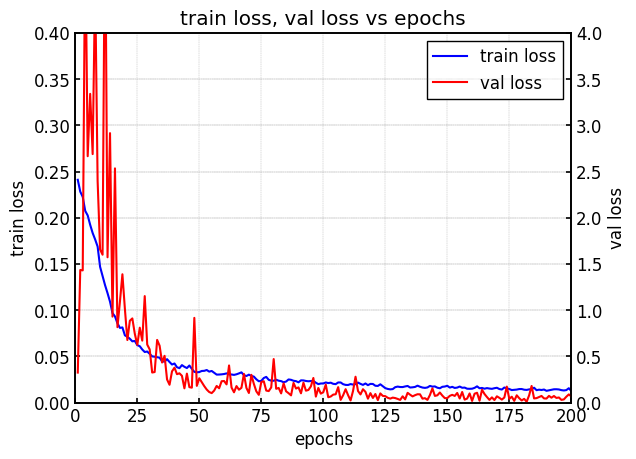 | 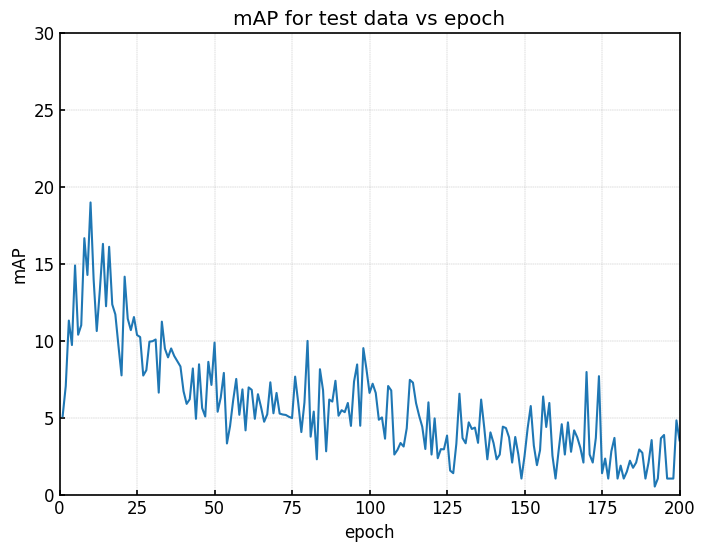 |
| (a) 学習時のval loss | (b) testデータのmAP |
Faster-R-CNNのモデルではtrain lossの値が低下するにつれて、val lossの値も低下しており、問題なく学習が進んでいるように思われる。
しかし、val lossが低下するにつれてmAPの値も低下している。
そのため、val lossの値を基準にモデルを選択すると、精度の低いモデルを選択することになる。
少なくともFaster-R-CNNに関しては、別の選択基準を検討する必要があります。
SSD
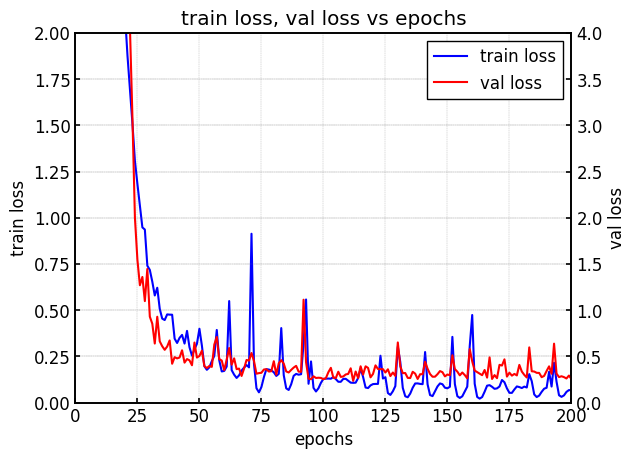 | 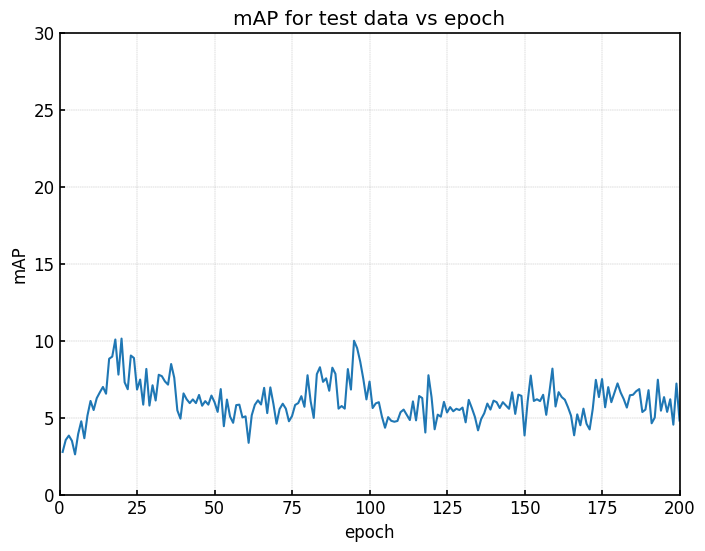 |
| (a) 学習時のval loss | (b) testデータのmAP |
SSDモデルのエポック数の小さい範囲では、val lossが小さくなるつれてmAPの値も高くなっている。
そのため、一見するとval lossの値とmAPの間に相関関係があるように見える。
詳細は後ほど。
YOLOv8
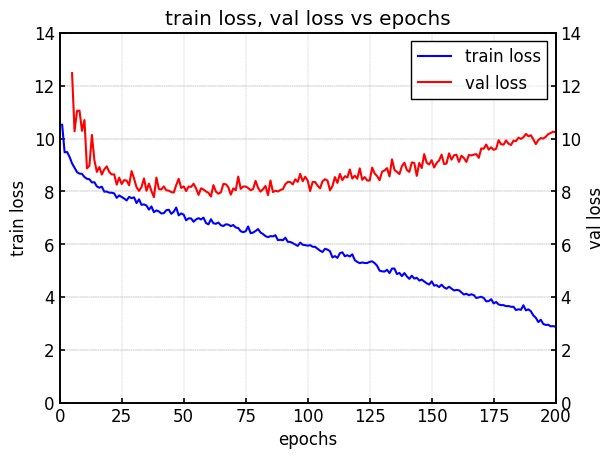 | 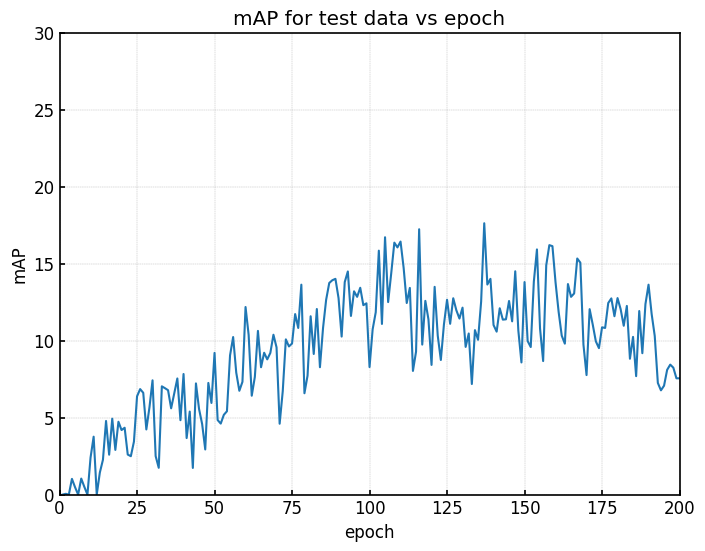 |
| (a) 学習時のval loss | (b) testデータのmAP |
YOLOv8では学習過程において、途中からval lossが増加しており、過学習が生じている。
mAPの値も同様に、あるエポック数から低くなっているように見える。
こちらもSSDと同様に一定の相関関係がみられるように思われる。
こちらも詳細は後ほど
モデルの選択基準② mAP(val data)とmAP(test data)
次は、valデータに対するmAPとtestデータに対するmAPの値の推移を比較していきます。
valデータ自体が学習時に使用しているものなので、一般にそれをmAPで評価することはあまり良くはないです。
しかし、なんらかの相関関係がみられる可能性もあるので検討していこうと思います。
Faster-R-CNN
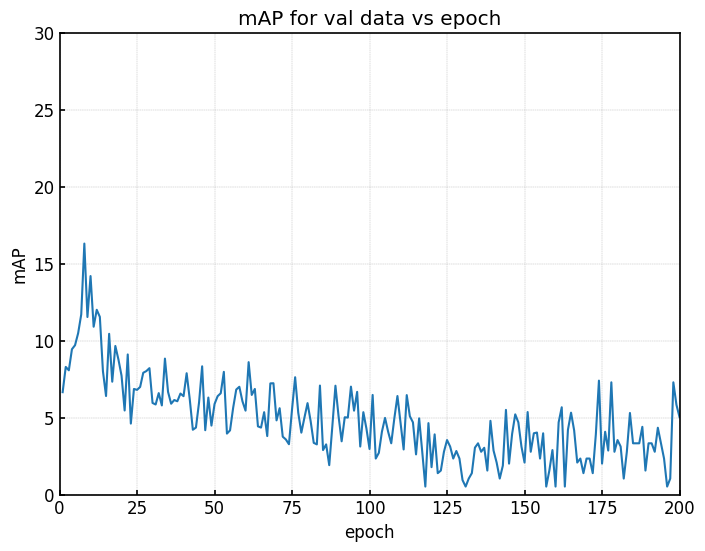 |  |
| (a) valデータのmAP | (b) testデータのmAP |
上図より、(a)valデータのmAPと(b)testデータのmAPの値の推移は非常に似ています。
ぱっと見ではありますが、ある程度の相関関係が期待できます。
SSD
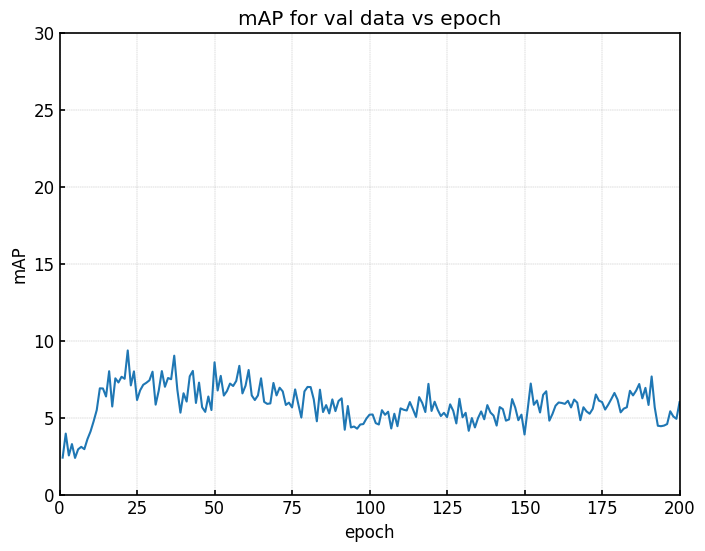 |  |
| (a) valデータのmAP | (b) testデータのmAP |
SSDもFaster-R-CNNと同様、(a)valデータのmAPと(b)testデータのmAPの値の推移が似ており、ある程度の相関関係が期待できます。
詳細は後ほど。
YOLOv8
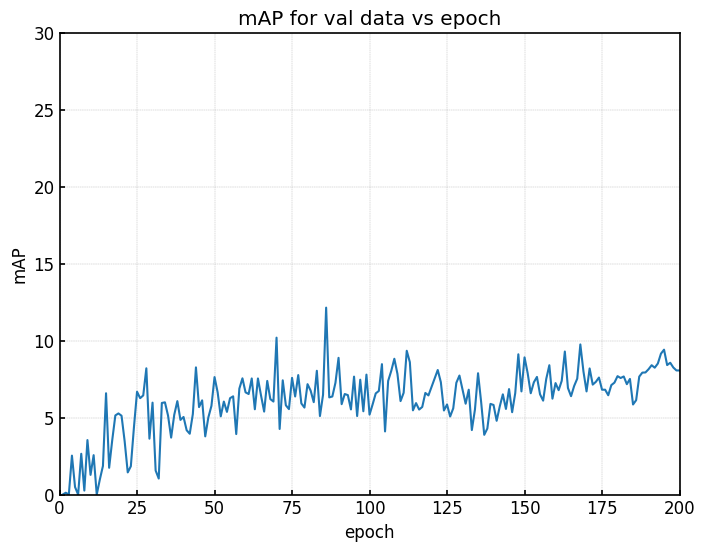 |  |
| (a) valデータのmAP | (b) testデータのmAP |
Faster-R-CNNやSSDと比較すると、YOLOはあまり相関関係が見られないように感じます。
詳細は後ほど。
モデルの選択基準の評価
評価方法
今回紹介した2パターンの選択基準について、定量的に評価を行っていきたい。
そこで、2パターンの選択基準を以下の方法で評価していく。
選択基準①(val lossとtestデータのmAP):
- val lossの値が最も小さいエポック数から、50番目までのエポック数を取得する。
- 同時に、testデータのmAPの値を大きい順に並べ、最も大きい値から50番目までのエポック数を取得する
- 上記の二つのデータの内、同じエポック数をどれだけ含んでいるか算出する
選択基準②(valデータのmAPとtestデータのmAP):
- valデータのmAPの値を大きい順に並べ、最も大きい値から50番目までのエポック数を取得する
- 同時に、testデータのmAPの値を大きい順に並べ、最も大きい値から50番目までのエポック数を取得する
- 上記の二つのデータの内、同じエポック数をどれだけ含んでいるか算出する
具体例
valデータのmAPとtestデータのmAP(Faster-R-CNN)の場合
step1:
エポック数ごとにvalデータのmAPを記載したmap.csvというファイルを読み込む。
その後、mAPの値が最も大きいエポック数から、50番目までのエポック数を取得してリストに格納。
map_csv_path = os.path.join(val_folder_path, 'map.csv')
map_result_df = pd.read_csv(map_csv_path)
map_val_index = map_result_df.nlargest(50, 'map')
map_val_index_list = map_val_index['epoch'].tolist()
print(map_val_index_list)[8.0, 10.0, 12.0, 7.0, 13.0, 9.0, 11.0, 6.0, 16.0, 5.0, 18.0, 4.0, 22.0, 34.0, 19.0, 61.0, 46.0, 2.0, 29.0, 3.0, 28.0, 14.0, 53.0, 27.0, 41.0, 20.0, 76.0, 174.0, 17.0, 178.0, 198.0, 69.0, 68.0, 84.0, 89.0, 94.0, 58.0, 26.0, 24.0, 63.0, 57.0, 25.0, 35.0, 96.0, 1.0, 32.0, 52.0, 39.0, 62.0, 101.0]step2
エポック数ごとにtestデータのmAPを記載したmap.csvというファイルを読み込む。
その後、mAPの値が最も大きいエポック数から、50番目までのエポック数を取得してリストに格納。
map_csv_path = os.path.join(test_folder_path, 'map.csv')
map_result_df = pd.read_csv(map_csv_path)
map_test_index = map_result_df.nlargest(50, 'map')
map_test_index_list = map_test_index['epoch'].tolist()
print(map_test_index_list)[10.0, 8.0, 14.0, 16.0, 5.0, 9.0, 21.0, 11.0, 13.0, 17.0, 15.0, 18.0, 24.0, 22.0, 3.0, 33.0, 7.0, 23.0, 12.0, 6.0, 25.0, 26.0, 31.0, 80.0, 30.0, 29.0, 50.0, 4.0, 19.0, 98.0, 36.0, 34.0, 37.0, 35.0, 38.0, 48.0, 45.0, 96.0, 39.0, 43.0, 99.0, 84.0, 28.0, 170.0, 53.0, 20.0, 27.0, 174.0, 76.0, 57.0]step3
最後に上記で作成した二つのリストから、値が一致する確率をパーセンテージで算出する。
match_count = sum(1 for elem in map_test_index_list if elem in map_val_index_list)
match_percentage = (match_count / len(map_test_index_list)) * 100
print(match_percentage)66.0この値が大きいほど、valデータのmAPとtestデータのmAPの間に相関関係があると言える。
この値自体に意味はなく、値を比較することで優劣を検討していきたい。
結果
Pattern1:val lossとmAP(testデータ)の相関関係
Pattern2:mAP(valデータ)とmAP(testデータ)の相関関係
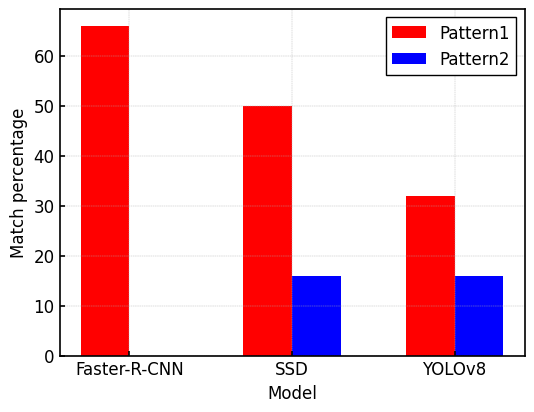
上記の結果より、Pattern2の方がPattern1よりも、testデータのmAPとの間に相関関係が見られる。
そのため、val lossの値を元にモデルを選択するよりも、valデータのmAPの値を元にモデルを選択する方が良いと言える。
特にFaster-R-CNNでは、valデータのmAPとtestデータのmAPの推移が一致していることが確認できた。
すべてのエポック数のモデルにおいて、Faster-R-CNNのval, testデータに対するmAPの値をそれぞれ横軸, 縦軸にプロットした図を下記に示す。
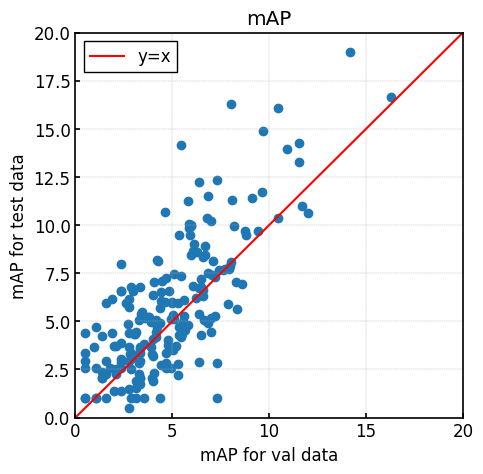
全体的にy=x上にデータがのっており、ある程度の相関関係があることが分かる。
総評
今回は2パターンでモデルの選択方法について検討していきました。
どちらかと言えば、パターン②の「valデータに対するmAP」の値がtestデータに対するmAPの値と相関関係が見られました。
特に、Faster-R-CNNのモデルではその傾向が顕著に表れており、実際にモデルを選択する際にも有用であると思われます。
今回はデータセットのデータ数が少なかったこともあり、train, val, testに分けたデータの中でモデルをうまく選択する方法について検討していきました。
データ数に余裕があれば、別のデータで各モデルの精度を比較した上で、testデータに使用するモデルを選択すると良いかもしれませんね。


コメント